para explorar as possibilidades e variações do que dar-lhe a fatia tamanho habitual.

Para apreciar o seu entusiasmo se não utilidade dos resultados, pode-se ter um olhar para um documento sobre arXiv por dois pesquisadores Joel Haddley e Stephen Worsley do Departamento de Ciências Matemáticas da Universidade de Liverpool.

O documento é intitulado "famílias infinitas de tilings disco monohedral" e eles têm explorado esta com referência à corte pizza.

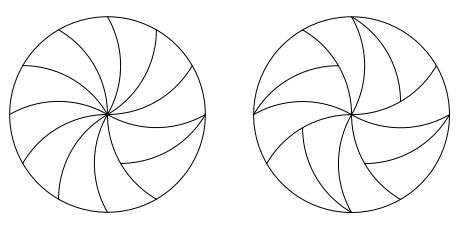
Para compreender como a pizza desempenha um papel no seu papel, pode-se voltar para a definição de uma telha monohedral como aquele em que todas as peças têm o mesmo formato, em que cada azulejo no lado a lado é congruente com um subconjunto fixo de avião. O conjunto é o prototile da telha, eo prototile admite a colocação de azulejos.

Os autores escreveram em seu papel: "A telha de uma forma planar é chamado monohedral se todas as peças são congruentes um ao outro Nós investigaremos a possibilidade de produzir tilings monohedral do disco Tais tilings são produzidos em uma base diária por chefs de pizza.. tomando cortes radiais distribuídas uniformemente ao redor do centro da pizza. Depois de construir este ladrilhos, um bairro da origem tem interseção não-trivial com cada telha ".

Eles novamente mencionou a questão principal de seu artigo: Podemos construir tilings monohedral do disco de tal forma que uma vizinhança da origem tem intersecção trivial com pelo menos uma telha?

Relatar esse papel, New Scientist teve uma história sexta-feira a manchete "Os matemáticos inventar nova forma de fatia da pizza em formas exóticas." Jacob Aron disse: "A maioria de nós dividir uma pizza com cortes retos que todos se encontram no meio. Mas e se o centro da pizza tem uma cobertura que algumas pessoas preferem evitar, enquanto outros querem desesperadamente crosta para mergulhar?"

Os matemáticos tinha vindo anteriormente com uma receita de corte conhecido como um disco telha monohedral, disse Aron, resultando em 12 peças em forma idêntica, seis das quais formam uma estrela que se estende para fora do centro, e os outros seis dividir o restante duro. "Você começa cortando fatias de três lados curvos em toda a pizza, em seguida, dividindo essas fatias em dois para obter o interior e grupos de fora", disse Aron.

"Eu não tenho nenhuma idéia se existem aplicações em tudo ao nosso trabalho fora de corte de pizza," disse Haddley em New Scientist. Ele tentou cortar uma pizza desta forma para o real. Mas os resultados são "interessantes matematicamente, e você pode produzir algumas imagens agradáveis."

As imagens não são apenas bom, mas como figuras que ilustram as formas e cortes alcançado em suas explorações de possibilidades de corte e, como disse o Popular Science, "Eles descobriram uma maneira de cortar peças cheias de curvas com quase um número infinito de lados (contanto que é uma número ímpar de lados) e, em seguida, dividir ainda mais essas fatias ao meio. " Os dois autores ainda mergulhou formas mais complexas; eles fizeram cunhas nas laterais disse Lindsey Kratochwill em Ciência Popular ", continua a produzir tilings monohedral que se encaixam em um círculo."

Na verdade, relativas ao exercício de cortar a pizza em discussões matemáticas não é nada novo. Como Gizmodo recordou-nos na sexta-feira, "O corte de pizza é um estranhamente bem pesquisado área da matemática, principalmente porque tem menos a ver com pizza e mais a ver com a geometria circular."

Jamie Condliffe disse: "O trabalho baseia-se em pesquisas anteriores que mostraram que era possível cortar uma pizza em seis fatias curvas (ou" escudos "), cada um dos quais poderiam então ser cortados ao meio para produzir 12 fatias idênticas."

Fornecido por: Da phys 2016 ( STOP)